ZES – Center for Emergent-law-based Statistics
ZES – Center for Emergent-law-based Statistics

Searching for patterns that were always true in the past in order to predict the future.
Emergent-law-based Statistics is a completely new approach to data analysis that is based on a purely empirical solution of the so called “epistemological induction problem”.
On the basis of this approach members of the ZES have developed algorithms that have the following two main characteristics:
-
They make predictions that reach at least the prediction accuracy of state of the art Machine-Learning-Algorithms but are perfectly intuitive.
-
They compile databases that contain objectively true empirical knowledge. It is important to realize that any statements derived from this knowledge cannot contradict each other.
What’s New?
See our latest presentations (in german) for the current status of our approach:
-
Emergent Law Based Statistics
“I think […] that mathematical ideas originate in empirics. But, once they are conceived, the subject begins to live a peculiar life of its own and is […] governed by almost entirely aesthetical motivations. In other words, at a great distance from its empirical source, or after much “abstract” inbreeding, a mathematical subject is in danger of degeneration.
Whenever this stage is reached the only remedy seems to me to be the rejuvenating return to the source: the reinjection of more or less directly empirical ideas.”
John von Neumann – “The Mathematician” in The Works of the Mind (1947)
In our opinion “probability” is such a degenerated concept.
There is neither an objective way (without any assumptions) to arrive at a probability statement from observations nor does the probability statement predict any possible concrete observation.
Taking the statement “if it has rained today, then the probability that it will rain tomorrow is equal to 60%” as an example, neither the statement can be objectively derived from observations nor can the statement as such be objectively and finally falsified.
In order to “reinject” empirical content into the fundament of statistical reasoning, we replace the concept of probability by the concept of “emergent laws”.
Emergent Laws are descriptions of patterns that always were observed in the past.
“In every sequence of 10 days (each following a rainy day) the relative frequency of rain was at least 60%.”
We call this an “emergent law” because we only state a feature (relative frequency) of sequences of measurements (10 measurements) was always observed and this is explicitly not a feature of a single measurement.
This law is also deterministic, because it states that some kind of complex but nevertheless exact observation has always been true until now. Taking into account that only what has always been true in the past can possibly be true in general emergent laws create the chance to make falsifiable predictions: “The relative frequency of rain in the next 10 days following a rainy day will be at least 60%.”
In case such a prediction is falsified once the falsified universal statement will remain false forever. If we can find enough not falsified deterministic laws and if we can identify general consequences from sequences of such predictions we can build up empirical science on a very solid methodological fundament.
Based on the methods of emergent-law-based statistics we found billions of emergent laws, in lots of databases. So there is no doubt that there are enough empirical laws to base statistics only on emergent laws.
Further the performance of the prediction strategy that a pattern that was always true until now, will appear again the next time, can be evaluated empirically and we found that certain patterns of prediction quality were always observed in lots of different prediction tasks, and as a consequence they can be described by emergent laws as well. We call laws about the universal performance (independent of the type of prediction task) of a prediction strategy Meta-Laws.
So we think that we solved the epistemological “induction problem”.
By applying emergent laws and meta-laws to statistical problems we found far reaching consequences:
-
-
-
-
Machine Learning (ML) Algorithms that search for emergent laws guided by meta-laws demonstrate a prediction performance at least comparable with the most advanced ML-Algorithms (e.g. Deep Neural Nets or XG-Boosting).
-
Because emergent laws and meta-laws were empirically true until now they never can contradict each other. So Databases containing knowledge defined by emergent laws can be easily combined without any limitation. A meaning-full kind of KnowledgeBase becomes possible.
-
A learning system that is based on a KnowledgeBase and evaluates the laws in real-time reveals aspects of the world that were always true until now.
-
-
-
Knowledge Nets - Creation of Knowledge
Resulting Solutions
Using emergent-law-based Statistics allows applications that are (in our assessment) not possible with probability based statistics.
KnowledgeBases
Because in probability based statistics it is always possible to make probability-statements about the same future observations (i.e. make predictions) on basis of different probabilistic theories (or methods) that cannot be true at the same time.
So as an example, we can use lots of sets of probabilistic assumptions and an infinity of estimation methods and surely claim that the probability of rain tomorrow is 0.4, 0.5 or any other probability value. At the same time it is impossible to prove one of the claims or theories definitively wrong.
So it seems to be impossible to collect empirical stochastic knowledge in a Database. In our reasoning there is no stochastic empirical knowledge and a database containing empirical results that are based on stochastic models could include an infinite number of conflicting statements.
One of the major advantages of emergent-law-based statistics therefore is the fact that emergent laws and the simple prediction rule “predict that a pattern that always was true in the past also will become true the next time” cannot result in conflicting predictions. So it becomes possible to collect consistent empirical knowledge in form of emergent laws in databases.
See the power of the resulting KnowledgeBases in the following example:
(Click on the image for fullscreen.)
Learning Systems
Because emergent-law-based statistics makes definitively falsifiable predictions, it becomes possible to evaluate the laws stored in a KnowledgeBase continuously if the predictions are compared to real-time measured data.
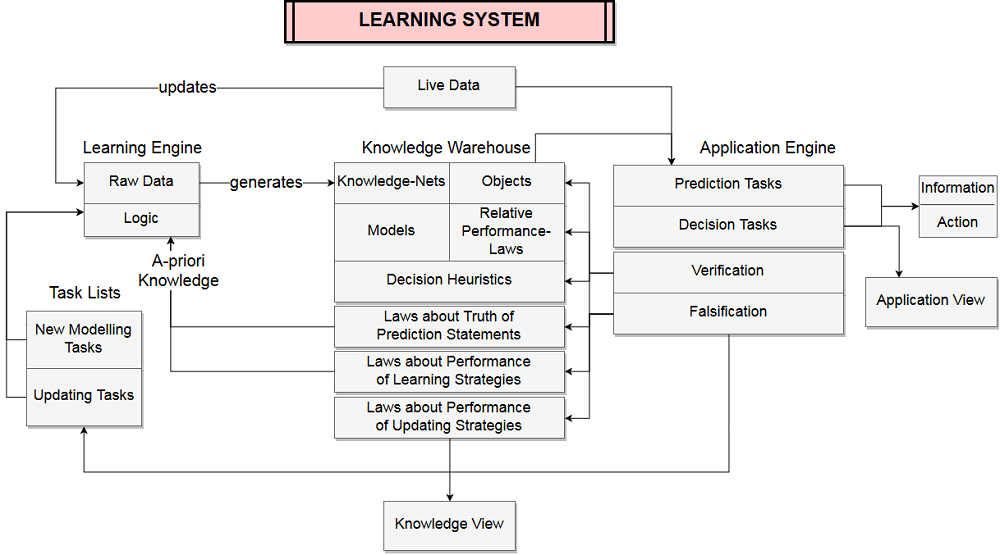
This leads to a system that – at every point in time – has knowledge about “what was always true until now”.
At each point in time each law in the KnowledgeBase of a Learning System can be falsified by measurements and the system is learning continuously and the resulting set of surviving laws reflects the actual state of knowledge.
The following graph shows the structure of a Learning System:
An Example of a Learning System is discussed in the following text.
Central Concepts
Click on Concept for more information.
Emergent Law
We define a pattern as a relation between functions of sequences of measurements. Any pattern which has never been falsified (and thus was always confirmed / always-true) is called an …
Meta Laws
Why is it useful to be able to find emergent laws? Can we judge how reliable the prediction, that an always-observed pattern will repeat, really is?
T-Dominance
If a decision rule A always led to better results compared to decision rule B after T decisions, we call rule A T-dominant against B.
KnowledgeNets
Sets of emergent laws that show the (well defined) complete set of relations of objects concerning one or several variables of interest.
Emergent Law Based Models
Knowledge stored in a KnowledgeNet is combined to solve prediction task evaluated with the usual metrics (Mean Absolute Prediction Error, AUC,…). The resulting models demonstrate a very high level of …
WorldViews
Knowledge stored in a KnowledgeNet is combined to show predictable features of several variables of interest. It shows interesting features of the world that have been always true until now. …
More Thorough Discussion and Presentation of our Approach
Notebooks and Papers
Notebooks
In this section we show preliminary results. Because our methods lead to very fast progress and lots of results we want to publish some of them without taking too much care on formal restrictions like ortography and so on. Please excuse possible errors in advance.
Papers
Papers provide further information with a more detailed explanation of our approach.
Contact
We believe in the enourmous social and commercial potential of our method.
If you are interested, do not hesitate to contact us.